【煤炭行业标准(MT)】 评定选煤厂重选设备工艺效果的计算机算法

1引言
中华人民共和国煤炭工业部部标准评定选煤厂重选设备工艺
效果的计算机算法
MT 145-86
1.1本标准规定了用计算机计算选煤厂中重介质分选机、跳汰机、选煤槽、斜槽分选机、摇床和旋流器等重选设备工艺效果评定指标的算法。这些指标包括可能偏差、不完善度、数量效率和错配物总量等。
与本标准有关的标准化文件：
MT/Z4一79《选煤厂重选设备工艺效果评定方法》，a.
国际标准ISO923《选煤试验结果的表示和说明》，GB478-80《煤炭浮沉试验方法》。c.
2分选产品产率的计算
在无实测数据的情况下，分选产品的产率可按附录A提供的算法计算。在完成产品产率和重产品分配率的计算之后，应该对计算所得的数据进行检验。发现下列情况2.2
之一时，则不能继续进行计算机处理。产品产率的计算结果中出现负值；a.
“计算原煤”与人选原煤各密度级产率的均方差超出MT/Z4一79的规定范围，“计算原煤”各密度级的平均灰分不能按平均密度构成递增序列。2.3出现2.2所列情形时，如果有相邻两密度级的“计算原煤”与人选原煤的产率差值的绝对值均大于2，且符号相反，允许将这两个密度级合并，重新进行计算。但任何情况下，密度级的总数都不允许少于6级。
3各密度级平均密度的确定
3.1中间密度级
3.1.1原煤或产品浮沉组成中第二个密度级至倒数第二个密度级的平均密度，根据质量守恒关系，按式（1）确定：
式中：—
-第i个密度级的平均密度，kg/L，Yi-Yi
第i个密度级的浮物累计产率，%，第（i～1）个密度级的浮物累计产率，%，-密度的倒数，可视为累计浮物产率Y的函数。中华人民共和国煤炭工业部1986-09-29发布（1）
1986-11-01实施
3.1.2函数关系：
用拉格朗日元三点插值公式分段确定。3.2端部密度级
MT 145-86
3.2.1第一个密度级的平均密度和最后一个密度级的平均密度一般按GB6949-86《煤炭视比重测定方法》确定。
3.2.2在不具备试验值的情况下，上述两个密度值可根据“计算原煤”的可选性数据，按中间诸密度级的平均密度对灰分的线性回归方程外推获得。3.2.3当第一个密度级平均密度的外推值高于浮沉试验的第一个密度时,第一个密度级的平均密度按下述原则取值：
当p,≥>1.3时，取p，=p,-0.02.当p1.3时，取p，=pf-0.01·
上两式中：p，——浮沉试验的第一个密度，kg/L，一第一个密度级的平均密度，kg/L。p
（3）
3.2.4对于按本节所述方法推算获得的端部密度值产生异议时，应补充试验，获得试验值。3.3虚拟密度值
根据需要，最低密度物的虚拟密度值（pmin）和最高密度物的虚拟密度值（pmx），可按第--个密度级和最后-一个密度级中物料对密度呈线性分布的假定，分别用以下两个式子推算：Pmin= 2 p,-
Pmax = 2 p,- Pn-
式中：P.——最后个密度级的平均密度，kg/L，Ph-t-
-浮沉试验的最后一个密度，kg/L。4可选性曲线的绘制原则
4.1原煤的可选性曲线以“计算原煤”的可选性数据为依据。(5）
4.2用以评定分选效果的可选性曲线，可以采用下列两种曲线之一。但推荐采用4.2.1的曲线。4.2.1迈耶尔曲线（M曲线）和密度曲线（曲线）。4.2.2浮物累计曲线（β曲线）和密度曲线（5曲线）。4.3可选性曲线~般应采用插值方法绘制，当插值方法不能获得足够光滑的曲线，在插值子区间内出现不适当的拐点时，允许采用性态适当的数学模型通过非线性拟合的方法获得曲线。4.4用插值方法处理可选性曲线时，应遵照下列规定：4.4.1采用分段连续的三次多项式插值方法（见附录B）。该方法的原则是：4.4.1.1在相邻的两个型值点之间建立一个三次多项式。4.4.1.2每个型值点左右两侧的三次多项式在该型值点处具有相同的函数值和--阶导数值。4.4.1.3三次多项式在型值点处的导数，指定取为过该型值点及左右相邻型值点所做二次抛物线在该型值点处的导数值。
4.4.2在迈耶尔曲线和密度曲线的第一个和最后个插值子区间，允许使用拉格朗日元三点插值公式描述曲线。
4.5在采用非线性拟合方法处理可选性曲线时，应充分注意所用数学模型的性态特征，以保证所得曲线能够符合可选性曲线的一般性态。当选用不同模型做拟合时，以拟合误差最小的模型做为选定模型。
4.6与可选性曲线有关的各项工艺效果指标（理论精煤产率、数量效率、灰分误差、理论分选密度及对应于理论分选密度±0.1含量）均根据可选性曲线的数学描述获取。482
5等误密度和错配物总量的确定
MT 145--86
损失曲线和污染曲线，用拉格朗日-一元三点插值公式分段描述。5.1
根据损失曲线和污染曲线的交点，确定等误密度和等误密度下的错配物总量。5.2
5.3对于损失曲线和污染曲线，可以仅做数学描述，而不绘制曲线图形。6分配曲线的绘制原则
6.1基本原则
分配曲线用非线性拟合方法确定。6.2型值点
6.2.1分配曲线的型值点分为基本型值点和虚拟型值点。6.2.2基本型值点的横坐标为按本标准第3章所述方法确定的各密度级的平均密度；纵坐标为相应各密度级的人料在重产品中的分配率。6.2.3基本型值点必须符合下列要求：a.
各密度级的分配率必须按平均密度构成单调非递减序列，分配率大于或小于50%的型值点的数目均不少于两个，具有分配率大于75%和小于25%的型值点。c
当基本型值点中分配率为0的型值点或分配率为100%的型值点多于两个时，在进行拟合之6.2.4
前，应将多余的基本型值点舍去。如基本型值点中缺少分配率小于2%或大于98%的型值点，应分别增设相应的虚拟型值点。6.2.5
虚拟型值点的横坐标分别设置于最低密度物的虚拟密度（pmn）处或最高密度物的虚拟密6.2.61
度（pm×）处，其分配率分别取为0或1（100%）。6.3数学模型
用以拟合分配曲线的数学模型可根据型值点的分布情况自由选择，但模型的性态应符合下列6.3.1
要求：
在拟合区间内，模型呈单调递增函数，a.
在拟合区间的两端，模型的导数值均应接近于0。b.
6.3.2下述两个模型可供参考采用：a.
反正切模型：
y=bo +b, arctg(b,(x - b,)].
b指数模型：
式中：
y=b。+b,expr-(b2 /x)b)
x—密度级的平均密度，
bab,-bzb-
一对应于平均密度的分配率，
-模型参数。
6.4模型参数的估计
6.4.1允许采用任何一种最优化计算方法搜寻模型参数。但对于大多数由初等函数构成的数学模型来说，阻尼最小二乘法（见附录C）可能收敛效果最好。6.4.2拟合运算中，以拟合误差做为选代过程的控制变量，即F
式中：F.-
-拟合误差，
N—密度级数，
Ei———第i个型值点的分配率，%N
(E,-y;
MT 145-86
y—第i个型值点的分配率拟合值，%。6.4.3不论选择何种数学模型用何种优化算法进行拟合运算，最终所得拟合误差均应小于5。6.5模型的选定
6.5.1对于指定的一组分配率型值点，当采用不同数学模型或以不同的优化算法进行拟合运算时，最终应按拟合误差最小的原则选定模型及其参数。2一侯模型选定，即用该模型的参数计算与分配曲线有关的各项工艺指标（分配密度、可能偏6.5.2
差和不完善度）
MT 145--86
附录A
计算分选产品产率的最优化算法（参考件）
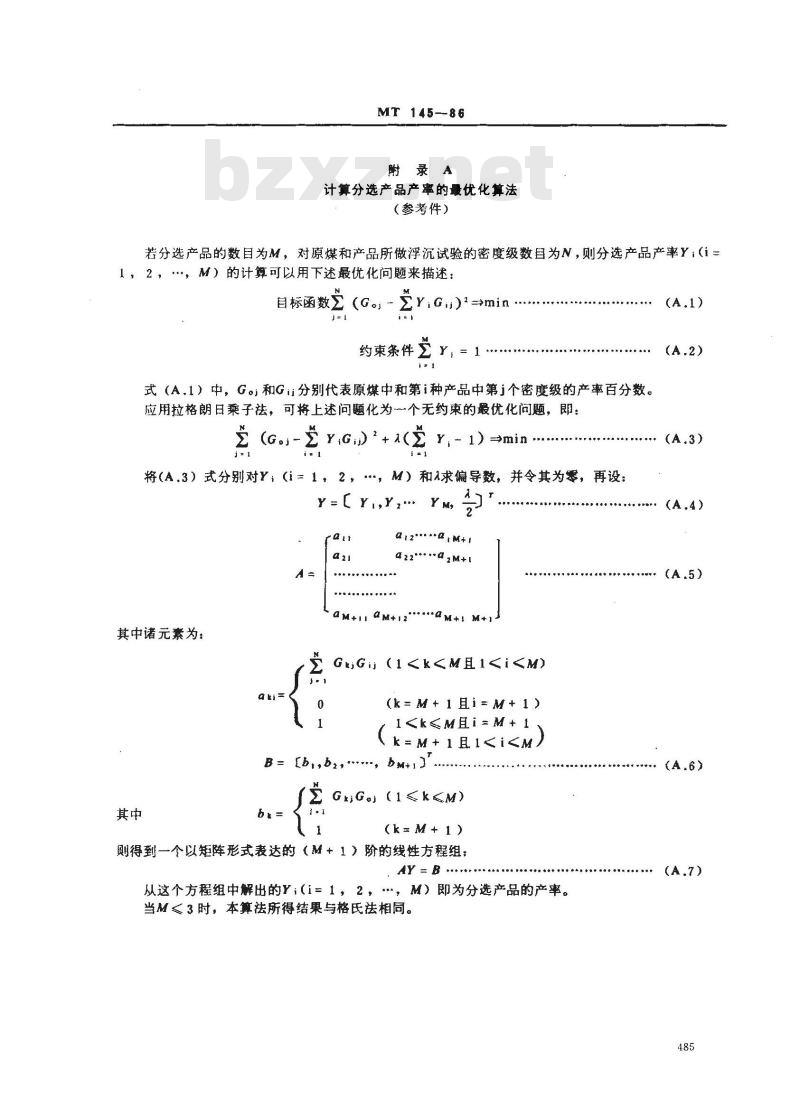
若分选产品的数目为M，对原煤和产品所做浮沉试验的密度级数目为N，则分选产品产率Y：（i=1，2，，M）的计算可以用下述最优化问题来描述：(G-
自标函数
ZY;Gu)1=min
约束条件艺
式（A，1）中，G。和Gu分别代表原煤中和第i种产品中第j个密度级的产率百分数。应用拉格朗日乘子祛，可将上述问题化为一个无约束的最优化问题，即：(Gi-
Y,- )=min.
将A.3）式分别对Y；（i=1，2，，M）和a求偏导数，并令其为零，再设：Y-Yi,Y, Ym,
其中诸元素为：
...am+I m+
am+1i am+i2..
GGij(1(k=M+ 1且i=M+ 1)
B= [b,b+,++, 办m+,]
E GrjG。j(1<(k=M+1)
则得到一个以矩阵形式表达的（M+1）阶的线性方程组：AY = B...
从这个方程组中解出的Y;（i=1，2，，M）即为分选产品的产率。
当M<3时，本算法所得结果与格氏法相同。(A.1)
MT 145--86
附录B
分段连续的三次多项式插值方法（参考件）
本方法的基本原则见正文4.4.1。实际计算可分为两步进行：
复。确定插值曲线在各个型值点处的斜率设有（N+1）个型值点（xj，yi）（j0，1，，N），则对于1≤j≤（N1）诸型值点可以做出通过该型值点及其左右相邻型值点的二次抛物线。抛物线方程的系数P，9，可由下述方程组中解出：
(pxi-i+qxj - +r = yj -1
pxi +qxj +r=yj
(pxi+i +qxj+i +r= yj+
根据所得到的抛物线方程的系数，就可以定出插值曲线在第j个型值点处的斜率M」，即：M,= 2 pxj +g
确定每两个相邻型值点之间的插值多项式b.
根据正文4.4.1所给出的原则，可以对1≤j≤（N－2）诸型值点为起点的插值区间建立三次插值多项式：
y=ax++bx- +cx+d..
这个多项式的系数可以根据第j个型值点和第（j+1）个型值点的函数值及导数值来确定。换句话说，多项式的系数a、b、c、d可由下述方程组解出：Iaxi +bxi +cxj +d=yi
axi++ +bxi++ + cxi++ +d= yj+t3axj +2bxy +c= Mj
3axi+I + 2bxi+1 + c= Mi+1
MT 145—86
附录C
估计模型参数的阻尼最小二乘法（参考件）
设有N个型值点（xk，J）（k=1，2，，N），并准备用数学模型y= f(x,bo,bi,*.*bm) ***
去进行拟合。
式（C.1）中，bo，b，bm可以用b（i=0，1，，m）表示，它们是非线性模型f的待定参数。这些参数需要用逐步逼近的方法去估计，现介绍如下：先给b；一个初始值，记为b!，并记初始值与真值（这是未知的）之差为4i，于是可以写出：bi =b?+ 4i(i= 0, 1,..,m)
.. (C.2)
这样，就可以把确定b,的问题化为确定修正盘4;的问题。为确定4i，可将函数（C.1）在b?附近做台劳级数展开，并略去4;的二次及二次以上的项，得：f(xx,bo,b,.bm)
式中, fi- f(xk,bo,bi,...bm)
af(x,bo,bt,.bm)
显然，当b给定后，f和
b。= b%
.(C.4)
都可以直接算出，利用（C.3）式，可以计算残差平方和Q*，即：Q
(yr- f(xt,bo,bi,...bm)]?
为了找出能使Q达到最小的一组参数b;（i = 0，1，ao
*残差平方和Q 与拟合误差F。的关系是：F。=VQ/N。afe
，m），各b；应满足如下的方程组：(C.6)
MT 145--86
即残差平方和对各参数b的偏导数皆为零。但
其中·
其中：
-（f+
4［4o,Ai,，
too tol
(yk-fe)
tio t++.....t+m
+t mr.*..-t+
(i,j=o，1
.，m)
G= [go,g.,..., gm?
(yk-fl)(i= 0,1,*,m)
则得用矩阵形式表达的线性方程组4m）（
.(C.8)
当型值点给定，并给出近似值b之后，矩阵T和向量G可分别按（C.9）式和（C.10）式算出。因此，可以从（C.11）中解出向量4。根据关系式（C.2）
bi =b?+ 4i(i= 0，1，.，m)
可以得到一组b，的新的近似值。如果4;的绝对值不是小得可以忽略不计，则可令当前的b；代替原来的b！，重复计算T和G，并解出新的4。如此反复选代，直至各4;的绝对值小于某个指定值或相邻两次送代的Q值差小于某个指定值时，最后所得到的b；即为所求的近似估计值。在实际计算中，若初始值b?取得不好，或模型函数的性态不好，则可能使一阶台劳展开式失真，造成选代过程不能收敛。因此，在求解方程（C。11）之前，应在矩阵T的主对角线诸元素上加上阻尼因子H，也就是用（1+H）（「i=j去代替tjli=j。H在迭代过程中应是变化的，在收敛的情况下，H可逐渐缩小，仅当不能保证相应的Q值比前次小的情况下，才加大H值。但H值也不能过大，当H>100时，可以改用b？+W4;求b，其中0D.1概述
MT 145--86
附录D
参考程序及其说明
（参考件）
D.1.1本程序仅做为阅读和使用本标准的参考。在执行本标准时，不要求必须按本程序进行计算。D.1.2本程序用PC-1500袖珍计算机BASIC语言写成。所有程序细节均按本标准之规定编写。运行时要求系统的内存容量至少要扩展到18k字节。D.2功能
本程序适用于计算多粒级多产品的重选工艺效果。在内存容量为18k字节的情况下，数据区的空间限定（粒级数×产品数×密度级数）小于等于120。如果数据区的空间不足以容纳所有粒级的浮沉试验数据，可以将所有粒级分为若干组，分别就每组中的各粒级做叠加，最后再叠加得到综合级。程序运行中，以彩色表格和彩色图形方式就综合级和各粒级输出下列结果：原煤和产品的浮沉组成表。
D2.2按最小二乘法原则计算的产品产率及分配率数据表。D.2.3
“计算产品”和“计算原煤”的浮沉组成表。“计算原煤”的可选性曲线。
D.2.5.按重产品分配率绘制的分配曲线。D.2.6工艺效果指标及有关的中间数据：分选产品的产率、“计算原煤”与“实际原煤”各密度级产率的均方差、等误密度、错配物总量、理论精煤产率、灰分误差、理论分选密度、理论分选密度下的±0.1含量，分配密度、可能偏差和不完善度。D.3程序框图
参考程序的总框图及若干主要子框图，见框图1～框图7。489
数据指针拨至 8000
分选方式变量X$，
粒度范圈变量L $，
粒级总数
产品总数
密度级总数
定义数组及工作单元
MT 145-86
输人浮沉试验密度序列
D(J)(J =1.2....N-1 J
形成表示溶度级范困的字符串数组D$ (J) (J =1.2.*.N)
调用处理多粒级数据的子程序
框图1总框图
输人原煤及各产品的粒度组成
T (I、K) (I=0,1,-M,
K= 1,2, -.-L J
调用处理多粒级数据的子程序
数据指针拨至8100
粒级由 1 至 V循环
调用处理多粒级数据的子程序
MT 145-86
T(T.1) 1EI=0,I...M)
粒级由 1 至 L 循环
输入粒度范围变量S 8
产品由0至M循环，
密度级由|至N循环
输人产事和灰分，计算它
们对综合级的质献并叠加
打印匾煤及产品的可选性
数据表格
用优化方法计算产品产率
计算并打印表格
“计算产品”的产率。
“计算原媒”的可选性数据”Www.bzxZ.net
*计算原煤”与实际原煤的
产率离差，
各分选阶段的分配率。
进行数据检验
验通让
计算并打印等误密度和
错配物总量
扩展端部密度值
绘制可选性曲线
计算与可选性曲线有关
的工艺指标井打印
绘制分配曲线
计算与分配曲线有关
的工艺指标并打印
处理多粒级数据的子程序
框图2
MT 145-86
2800开始
计算精煤的沉物果计分布，
获得污染曲线型值点坐标
计算重产品的浮物案计分布。
获得损失曲线型候点坠标
找出污染曲线与拟失曲线
交点所在区间
用拉格朗旦一元三点插值公式
找比交点的坐标
计算等误密度和错配物总睡
打印上述结果
框图3计算等误密度和错配物总量
小提示：此标准内容仅展示完整标准里的部分截取内容，若需要完整标准请到上方自行免费下载完整标准文档。